| Strona główna | Mapa serwisu | English version |
 |  |
 Wprowadzenie |
Tabela wartości trygonometrycznych |
Ćwiczenia i zadania |
Spis Treści |
KSIĘGA GOŚCI |
| Wprowadzenie > 1. Funkcje trygonometryczne kąta ostrego. |
Funkcje trygonometryczne kąta ostrego
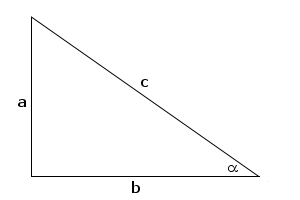
Definicja:
*sinusem kąta α nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej
sinα = a / c
* cosinusem kąta α nazywamy stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.
cosα= b / c
*tangensem kata α nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przyprostokątnej leżacej przy tym kącie.
tgα= a / b
*cotangensem kąta α nazywamy stosunek długości przyprostokątnej leżącej przy kącie do długości przyprostokątnej leżącej naprzeciwko tego kąta,
ctgα= b / a
Definicja:
*sinusem kąta α nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej
sinα = a / c
* cosinusem kąta α nazywamy stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.
cosα= b / c
*tangensem kata α nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przyprostokątnej leżacej przy tym kącie.
tgα= a / b
*cotangensem kąta α nazywamy stosunek długości przyprostokątnej leżącej przy kącie do długości przyprostokątnej leżącej naprzeciwko tego kąta,
ctgα= b / a
Dla ułatwienia można sobie skojarzyć, że:
- sinus i cosinus mają wspólny mianownik, przykład dla boków a=4 b=6 c=8
sinα= 4 / 8 = 1 /2
cosα= 6 / 8 = 3 /4
- sinus i tangens mają wspólny licznik, przykład:
sinα= 4 /8 = 1 /2
tgα = 4 /6 = 2 /3
- cosinus i cotangens mają wspólny licznik, przykład:
cosα= 6 /8 = 3 /4
ctgα= 6 /4 = 3 /2 = 1 1/2
- cotangens jest odwrotnościa tangensa, przykład:
tgα = 4 /6= 2 /3
ctgα= 6/4 = 3 /2
| To jest stopka |
